Ang Hippocrates ng Chios (fl. C. 460 bc) ay nagpakita na ang mga lugar na hugis ng buwan sa pagitan ng mga pabilog na arko, na kilala bilang mga lunes, ay maaaring maipahayag nang eksakto bilang isang lugar ng rectilinear, o kuwadrante. Sa sumusunod na simpleng kaso, ang dalawang lunes na binuo sa paligid ng mga gilid ng isang kanang tatsulok ay may pinagsama na lugar na katumbas ng sa tatsulok.
-
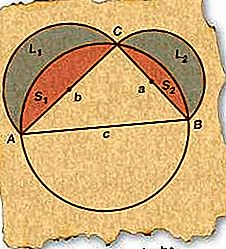
Simula sa tamang ΔABC, gumuhit ng isang bilog na ang diameter ay magkatugma sa AB (gilid c), ang hypotenuse. Dahil ang anumang tamang tatsulok na iginuhit gamit ang diameter ng bilog para sa hypotenuse nito ay dapat na isulat sa loob ng bilog, ang C ay dapat na nasa bilog.
-
Gumuhit ng mga semicircles na may diameters AC (side b) at BC (side a) tulad ng sa figure.
-
Lagyan ng label ang nagreresultang lunes L 1 at L 2 at ang mga nagreresultang mga segment S 1 at S 2, tulad ng ipinahiwatig sa figure.
-
Ngayon ang kabuuan ng mga lunes (L 1 at L 2) ay dapat na katumbas ng kabuuan ng semicircles (L 1 + S 1 at L 2 + S 2) na naglalaman ng mga ito minus ang dalawang mga segment (S 1 at S 2). Sa gayon, L 1 + L 2 = π / 2 (b / 2) 2 - S 1 + π / 2 (a / 2) 2 - S 2 (dahil ang lugar ng isang bilog ay π beses sa parisukat ng radius).
-
Ang kabuuan ng mga segment (S 1 at S 2) ay katumbas ng lugar ng kalahating bilog batay sa AB minus ang lugar ng tatsulok. Sa gayon, S 1 + S 2 = π / 2 (c / 2) 2 - ΔABC.
-
Pagsusulat ng pagpapahayag sa hakbang 5 hanggang hakbang 4 at pagpapatunay ng mga karaniwang termino, L 1 + L 2 = π / 8 (isang 2 + b 2 - c 2) + ΔABC.
-
Dahil ang ∠ACB = 90 °, isang 2 + b 2 - c 2 = 0, ng teorema ng Pythagorean. Sa gayon, L 1 + L 2 = ΔABC.
Ang Hippocrates ay pinamamahalaang upang parisukat ng maraming uri ng mga lunes, ang ilan sa mga arko ay mas malaki at mas mababa kaysa sa mga semicircles, at siya ay nagpakilala, kahit na maaaring hindi siya naniniwala, na ang kanyang pamamaraan ay maaaring parisukat sa buong bilog. Sa pagtatapos ng klasikal na edad, Boethius (c. Ad 470-524), na ang mga pagsasalin ng Latin ng mga snippet ng Euclid ay magpapanatili ng ilaw ng geometry flickering para sa kalahating libong milenyo, binanggit na may isang tao na nakamit ang pag-squaring ng bilog. Kung ang hindi kilalang henyo na ginamit lunes o ilang iba pang pamamaraan ay hindi kilala, dahil sa kakulangan ng puwang na si Boethius ay hindi nagbigay ng demonstrasyon. Sa gayon ay ipinadala niya ang hamon ng kuwadrante ng bilog kasama ang mga fragment ng geometry na tila kapaki-pakinabang sa pagsasagawa nito. Ang mga taga-Europa ay pinananatiling mabuti sa walang pasubali na gawain sa Enlightenment. Sa wakas, noong 1775, ang Paris Academy of Sciences, na pinangalagaan ang gawain ng paghanap ng mga fallacy sa maraming mga solusyon na isinumite sa ito, ay tumanggi na magkaroon ng anumang karagdagang gawin sa mga squarers ng bilog.